Two-disk-rollers

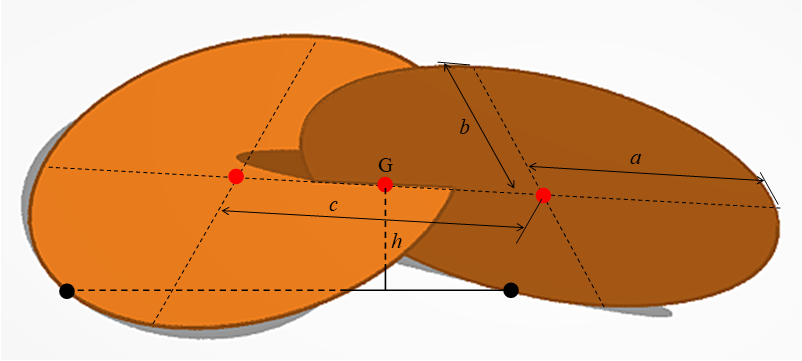
長半径\(a\)，短半径 \(b\) の楕円板（厚さは \(0\) ）を２枚，互いに垂直に，長軸上で組み合わせた構造物を考えます．任意の回転角で，床面からの重心の高さ \(h\) が一定になる条件は，楕円板中心間の距離を \(c\) として，

\[\tag{1} c^2=4 a^2 – 2 b^2\]

となります．このとき，重心の高さは，\(h=b/\sqrt{2}\) です．この構造物が平らな床面上で転がるとき，重心が左右に振れる面白い動きをします．そのため，Wobblersと呼ばれているようです．

上の式が成り立つには，\(a\ge b/\sqrt{2}\) ですが，等号が成り立つとき，\(c=0\) となり，円柱を軸に対して45度傾いた断面形状の楕円の組み合わせになります．転がるときの重心の運動は直線運動になります．

円板の場合，\(a=b=r\) として，\(c=\sqrt{2}\ r\) となります．

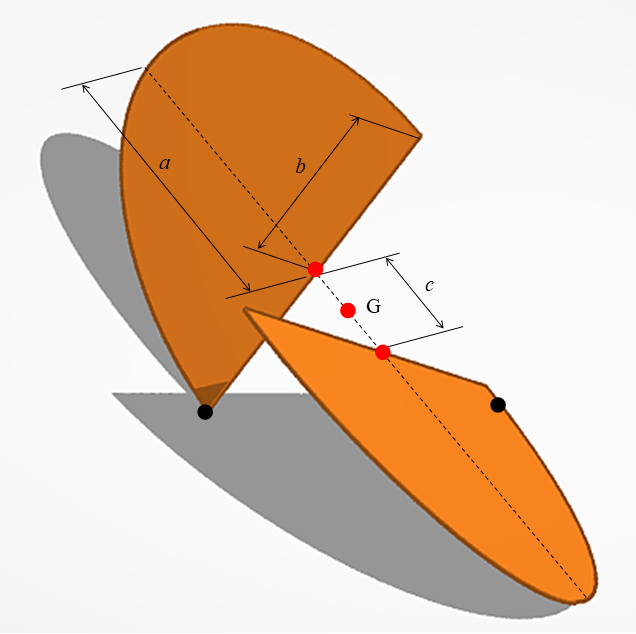
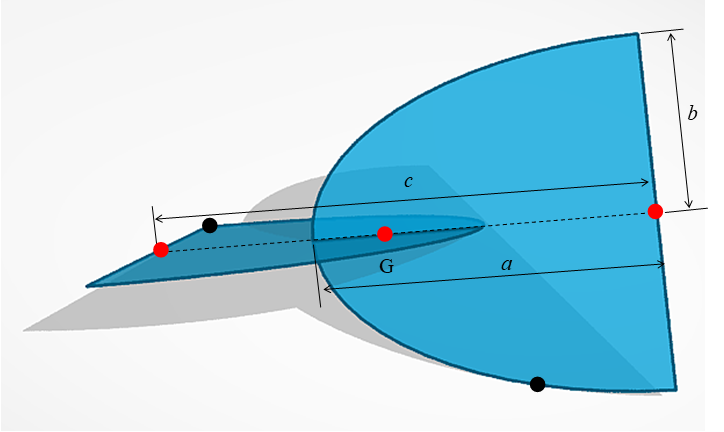
次に，短軸で切断された楕円の半分を２枚，互いに垂直に，長軸上で組み合わせた構造物を考えます．この場合は，一方の外周が床に接しているとき，片方の半楕円の短軸の端が常に同じ場所で床に固定された状態になります．そのため，重心の高さ \(h\) が一定になる条件は，

\[\tag{2} c^2=2 a^2 – 2 b^2\]

となります．ここで，\(a\ge b\) です．また，\(a\) と \(b\) は楕円の長軸半径，短軸半径，\(c\) は楕円中心間の距離です．重心の高さは，\(h=b/\sqrt{2}\) です．

半円の場合，\(a=b\) なので，\(c=0\) となります．全楕円板では，\(\pm c\) は区別がありませんが，半楕円板では別の構造になります．つまり，\(c \le 0\) も解になります．